수학과의 개발자 도전기

공부한 날짜: 2021. 10. 26 

-힙: 힙 순서 속성(Heap Order Property)을 만족하는 완전 이진 트리

-완전 이진 트리: 최고 깊이를 제외한 모든 기이의 노드들이 완전히 채워져 있는 이진트리

-힙 순서 속성: 트리 내의 모든 노드가 부모 노드보다 커야한다는 규칙

-힙이 보장하는 한가지 특성: '힙에서 가장 작은 데이터를 갖는 노드는 루트 노드이다.'

-삽입 연산

1. 힙 최고 깊이 최 우측에 노드 추가. 이때 힙은 완전 이진트리 유지

2. 부모노드와 비교해서 크면 멈추고, 작으면 다음 단계

3. 부모노드와 삽입 노드 바꾸고, 2번 진행

핵심은 새로 추가한 노드가 힙 순서 속성을 만족시킬 때따깆 부모노드와 계속해서 교환해 나가는 것 

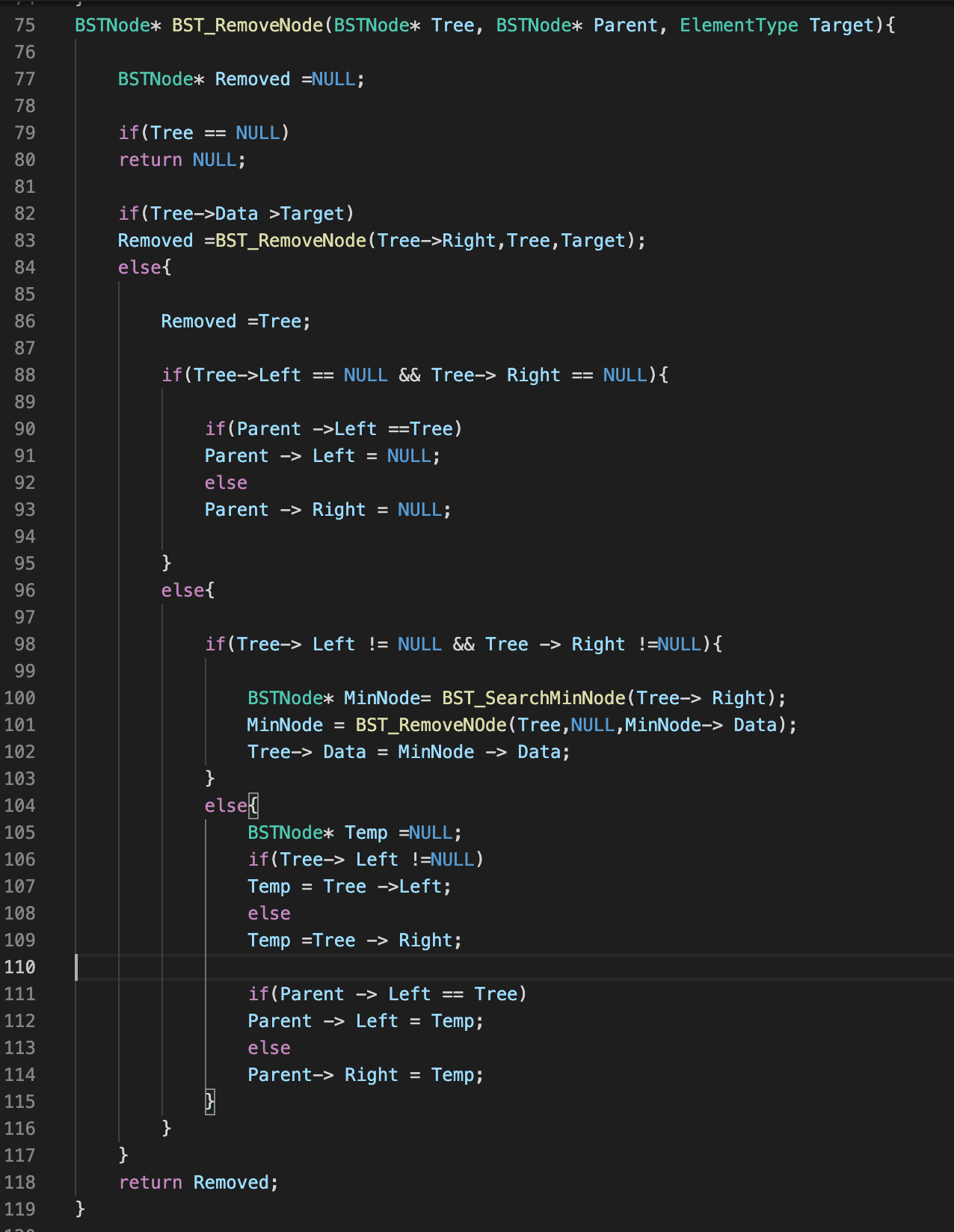
-삭제 연산(여기서는 힙의 최소값, 루트노드 삭제)

여기서도 노드 삭제 후 뒤처리가 주요 내용

*뒤처리 과정

1. 힙의 루트에 최고 깊이, 최 우측에 있던 노드를루트 노드로 옮겨온다.

2. 옮겨온 노드의 양쪽 자식을 비교하여 작은쪽 자식과 위치 교환

3. 힙 순서 속성 만족하면 멈추고, 아니면 2번부터 반복한다 

-힙의 구현 

힙에 사용하는 자료구조로는 배열이 더 낫다고 함 

완전 이진 트리를 배열로 나타내는 방법: 깊이 n의 노드는 배열의 (2^n -1) ~ 2*(2^n -1)번 요소에 저장한다 

이 배열의 장점: 배열 인덱스 만으로 힙의 각 노드 위치, 부모/자식 관계를 한번에 알아낼 수 있다 

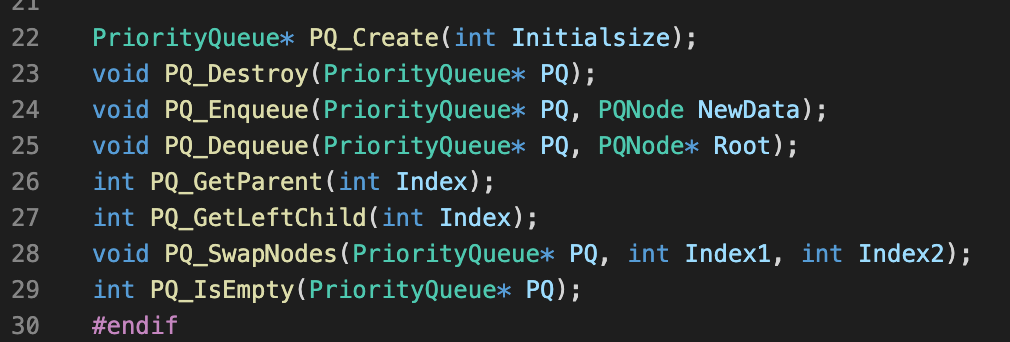
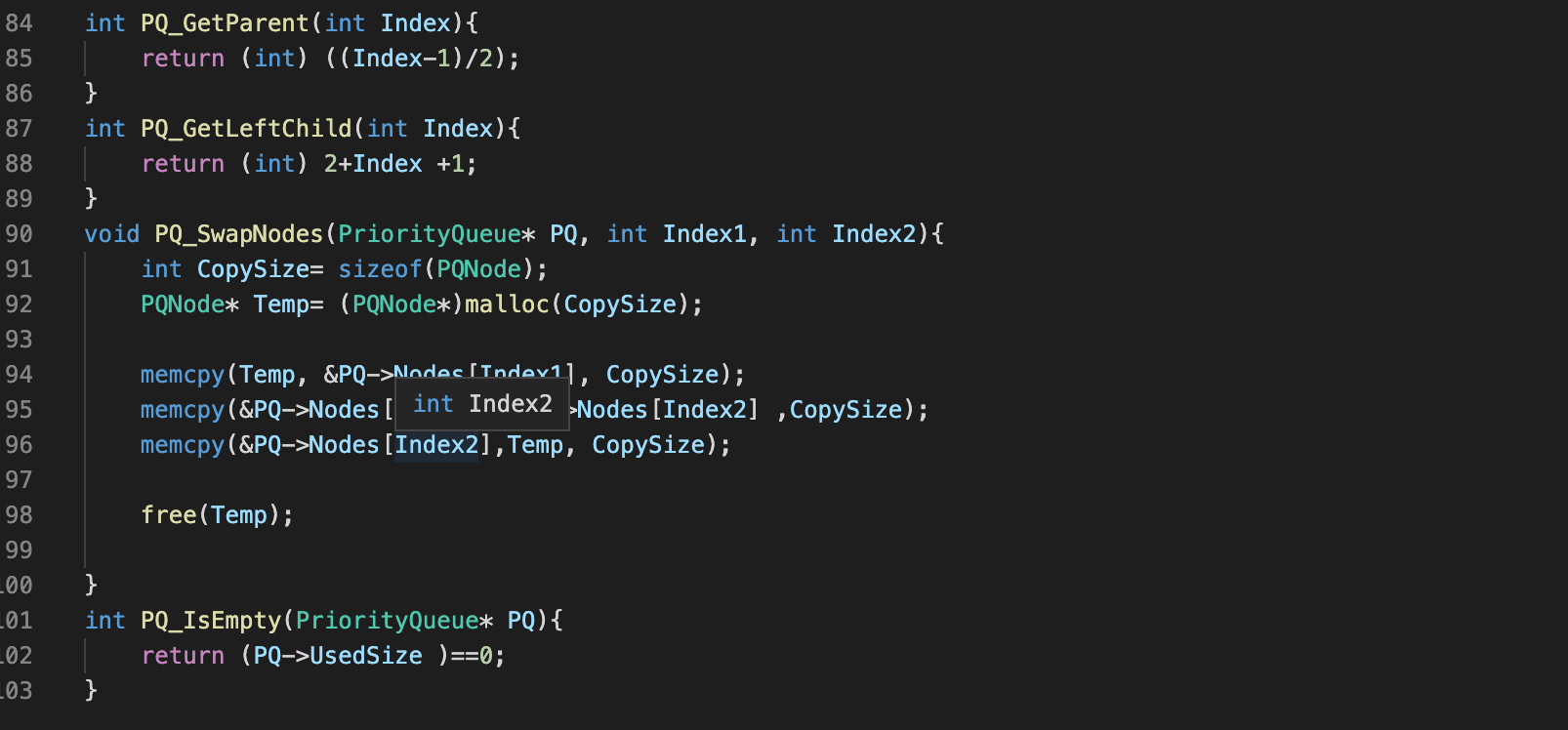
* k번 인덱스에 위치한 노드의 양쪽 자식 노드들이 위치한 인덱스

왼쪽 자식 노드: 2k+1, 오른쪽 자식 노드 2k+2

*k번 인덱스에 위치한 노드의 부모 노드가 위치한 인덱스: (k-1)/2의 몫 

공부한 날짜: 2021. 10. 26

-큐: fifo,lifo등의 자료구조를 일컬어 부르는 말

-우선순위 큐: 삽입(enqueue)과 제거(dequeue) 연산을 지원하는 자료구조. 

우선순위 큐를 통해 데이터 우선순위에 따라 출력 순서가 결정된다.  

핵심은 데이터 입/출력이 이루어질 때마다 최소한의 비용으로 최우선순위의 데이터를 헤드에 위치시키는 알고리즘의 효율이다 

-힙으로 우선순위 큐 구현하기 

-이진 탐색 트리: 이진 탐색을 위한 이진트리이다.

??: "이진 탐색 알고리즘이 있는데 왜 이진 탐색 트리가 필요?"

-> 이진 탐색은 데이터 집합이 배열인 경우에만 사용가능하다.(사전에 정의된 크기의 데이터 닙합에 대해서만 사용이 가능하고, 동적으로 그 크기가 달라지는 데이터 집합(예를 들어 링크드리스트)에는 적용이 불가능하다)

-이진 탐색트리 노드 규칙

: 왼쪽 자식 노드는 나보다 작고, 오른쪽 자식 노드는 나보다 크다. 

1. 이진 탐색트리 노드 정의 

2. 함수 정의 

3. 이진탐색트리 생성 

4. 이진탐색트리 노드 삭제 

5. 이진탐색트리 삭제 

6. 이진탐색트리 노드 찾기 

7. 이진탐색트리 최소값 노드 찾기 

8. 이진탐색트리 노드 삽입 

: 이진 탐색트리에서 노드 삽입 연산은 '새 노드가 삽입될 곳은 어디인가'를 찾아내는 거시 핵심이다.

새 노드가 삽입될 곳을 이진탐색으로 찾아야한다. 

9. 이진 노드탐색 노드 삭제 

: 삭제 과정이 삽입 과정보다 더 복잡하다. 

과정 1) 삭제할 노드를 찾아야한다. 2) 노드를 트리에서 떼어낸다.(노드의 상황에 따라서 뒷정리하는 과정 달라짐. 첫번째는 양쪽 자식 노드를 모두 갖고 있는 경우, 다른 하나는 왼쪽/ 오른쪽 중 어느 한쪽 자식 노드만 갖고 있는 경우)

자식 트리가 있는 노드를 삭제할 때 그 빈자리에 무엇으로 채워야할까?

->삭제된 노드의 오른족 하위트리에서 가장 작은 값을 가진 노드를 삭제 노드의 위치에 옮겨 놓는다. 

10. 이진탐색트리 전위법?으로 출력

• 이진탐색: 탐색 범위를 1/2씩 줄여나가는 알고리즘

• 과정

1. 데이터 집합의 중앙에 있는 요소를 고른다.

2. 중앙 요소의 값과 찾고자 하는 목표 값을 비교.

3. 목표값 < 중앙값 이면 중앙값 왼편 탐색/ 목표값 > 중앙값이면 중앙값 오른편 탐색

4.  목표값이 나올때까지 1~3과정 반복 

• 이진 탐색의 반복 횟수(데이터 개수 n개일 때) : log2n

-> 데이터 집합의 크기가 아무리 커져도 탐색 소요 시간은 아주 미미하게 증가한다는 것을 의미

**이진탐색 그냥 구현한 것도 작성해서 올리기**

• bsearch()함수로 이진탐색 구현